|
Es ist zu beweisen, daß die Zahl 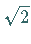 keine rationale Zahl ist.
Angenommen,
keine rationale Zahl ist.
Angenommen, 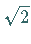 sei rational.
Dann gilt
sei rational.
Dann gilt 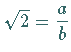 mit ganzen Zahlen
mit ganzen Zahlen 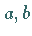 und
und 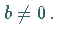 Die Zahlen
Die Zahlen 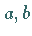 sind dabei teilerfremd , d.h., sie besitzen keinen gemeinsamen
Teiler.
Man erhält
sind dabei teilerfremd , d.h., sie besitzen keinen gemeinsamen
Teiler.
Man erhält 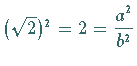 oder
oder 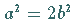 ,
d.h., ,
d.h., 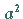 wäre
eine gerade Zahl, was nur dann möglich ist, wenn
wäre
eine gerade Zahl, was nur dann möglich ist, wenn 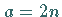 eine gerade Zahl ist.
Es müßte dann wegen
eine gerade Zahl ist.
Es müßte dann wegen 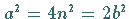 auch
auch 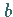 eine gerade Zahl sein.
Das ist offensichtlich ein Widerspruch zur Voraussetzung, daß
eine gerade Zahl sein.
Das ist offensichtlich ein Widerspruch zur Voraussetzung, daß 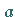 und
und 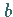 teilerfremd
sind.
teilerfremd
sind.
|