Tautologien, mathematische Schlußweisen
Ein aussagenlogischer Ausdruck heißt allgemeingültig oder
Tautologie , wenn er die Wahrheitsfunktion identisch W repräsentiert.
Folglich sind zwei Ausdrücke  und
und 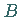 genau dann logisch äquivalent, wenn der
Ausdruck
genau dann logisch äquivalent, wenn der
Ausdruck  eine Tautologie ist.
Mathematische Schlußweisen folgen aussagenlogischen Gesetzen.
Als Beispiel sei das Kontrapositionsgesetz genannt, d.h. der allgemeingültige
Ausdruck
eine Tautologie ist.
Mathematische Schlußweisen folgen aussagenlogischen Gesetzen.
Als Beispiel sei das Kontrapositionsgesetz genannt, d.h. der allgemeingültige
Ausdruck
 |
(5.19a) |
Dieses Gesetz, das auch in der Form
 |
(5.19b) |
notiert werden kann, läßt sich wie folgt interpretieren:
Um zu zeigen, daß 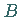 aus
aus  folgt, kann man auch zeigen, daß
folgt, kann man auch zeigen, daß 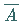 aus
aus 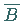 folgt.
Der indirekte Beweis beruht auf folgendem Prinzip:
Um
folgt.
Der indirekte Beweis beruht auf folgendem Prinzip:
Um 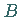 aus
aus  zu folgern, nimmt man
zu folgern, nimmt man 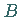 als falsch an und leitet daraus - unter der
Voraussetzung, daß
als falsch an und leitet daraus - unter der
Voraussetzung, daß  richtig ist - einen Widerspruch her.
Formal läßt sich dieses Prinzip auf verschiedene Weise durch aussagenlogische
Gesetze beschreiben:
richtig ist - einen Widerspruch her.
Formal läßt sich dieses Prinzip auf verschiedene Weise durch aussagenlogische
Gesetze beschreiben:
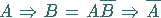 |
(5.20a) |
oder
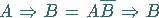 |
(5.20b) |
oder
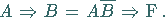 |
(5.20c) |