Lineare partielle Differentialgleichungen 2. Ordnung mit konstanten Koeffizienten
Wenn die Koeffizienten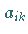 
in (9.83) konstant sind, dann
ist durch eine lineare homogene Transformation der unabhängigen Variablen eine
Transformation auf die einfachere Normalform
 |
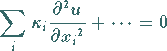(9.84) |
möglich, in der sämtliche Koeffizienten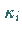 
gleich 
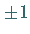oder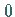 
sind.
Man kann mehrere charakteristische Fälle unterscheiden:
1. Elliptische Differentialgleichung Alle Koeffizienten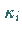
sind
von Null verschieden und haben dasselbe Vorzeichen: Dann handelt es sich um eine
elliptische Differentialgleichung .
2. Hyperbolische und ultrahyperbolische Differentialgleichung
Alle Koeffizienten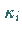
sind von Null verschieden, aber einer hat ein zu
allen übrigen entgegengesetztes Vorzeichen: Dann handelt es sich um eine
hyperbolische Differentialgleichung .
Treten darüber hinaus von jeder Vorzeichenart wenigstens zwei auf, dann ist es eine
ultrahyperbolische Differentialgleichung .
3. Parabolische Differentialgleichung
Einer der Koeffizienten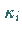
verschwindet, die übrigen sind verschieden
von Null und haben gleiches Vorzeichen: Dann handelt es sich um eine
parabolische Differentialgleichung .
4. Einfach zu lösender Fall
Ein relativ einfach zu lösender Fall liegt vor, wenn nicht nur die Koeffizienten
der höchsten Ableitungen der unbekannten Funktion konstant sind, sondern auch
die der ersten Ableitungen.
Man kann dann die Glieder mit den ersten Ableitungen durch eine Variablensubstitution
eliminieren, für die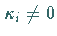 
ist.
Dazu setzt man
 |
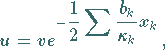(9.85) |
wobei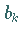 
der Koeffizient von 
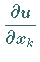in
(9.84) ist und die Summation über alle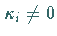
zu erfolgen hat.
Auf diese Weise können alle elliptischen und hyperbolischen Differentialgleichungen mit
konstanten Koeffizienten auf eine einfache Form gebracht werden:
a) Elliptischer Fall
 |
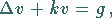(9.86) |
b) Hyperbolischer Fall
 |
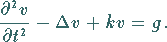(9.87) |
Mit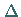 
wird der LAPLACEsche Operator
 |
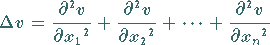(9.88) |
bezeichnet.
