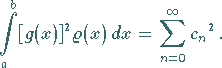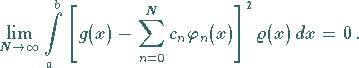Nichtsinguläre Fälle
1. Normierung der Eigenfunktion:
Zu jedem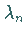 
wird eine Eigenfunktion 
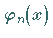derart gewählt, daß gilt
 |
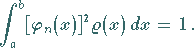(9.66a) |
Man spricht dann von einer normierten Eigenfunktion .
2. FOURIER-Entwicklung:
Jeder im Intervall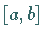 
definierten Funktion 
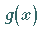kann ihre FOURIER-Reihe
 |
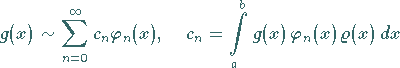(9.66b) |
nach den Eigenfunktionen des zugehörigen Randwertproblems zugeordnet werden, sofern die
Integrale in (9.66b) sinnvoll sind.
3. Entwicklungssatz:
Die FOURIER-Reihe konvergiert absolut und gleichmäßig gegen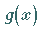 
,
wenn
die Funktion
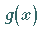eine stetige Ableitung besitzt und den Randbedingungen des
zugehörigen Problems genügt.
4. Parsevalsche Gleichung:
Wenn das Integral auf der linken Seite einen Sinn hat, dann gilt stets
 |
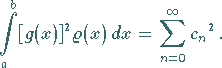(9.66c) |
Die FOURIER-Reihe der Funktion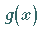
konvergiert in diesem Falle im Mittel gegen
,
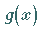d.h., es gilt
 |
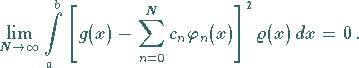(9.66d) |
