Dreidimensionale Wärmeleitungsgleichung
Die Ausbreitung der Wärme in einem homogenen Medium wird durch die lineare partielle
Differentialgleichung zweiter Ordnung vom parabolischen Typ
 |
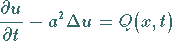(9.106a) |
beschrieben, wobei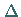 
der LAPLACE-Operator ist, hier
beschränkt auf maximal drei Ausbreitungsrichtungen 
,
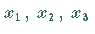beschreibbar auch durch den Ortsvektor 
.
Wenn der Wärmestrom weder Quellen noch Senken besitzt, verschwindet die rechte Seite
wegen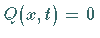 
.
Das CAUCHYsche Problem kann folgendermaßen gestellt werden: Es ist eine für
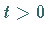beschränkte Lösung 
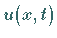zu suchen, wobei 
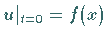sein soll.
Die Forderung nach der Beschränktheit sichert gleichzeitig die Eindeutigkeit der
Lösung.
Für die homogene Differentialgleichung mit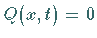 
erhält man die
Wellenfunktion
Für die inhomogene Differentialgleichung mit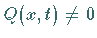 
ist auf der rechten Seite
dieser Gleichung der folgende Ausdruck zu addieren:
| |
|
 |
|
| |
|
 |
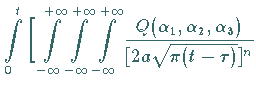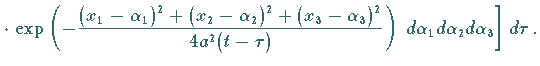(9.106c) |
Die Aufgabe,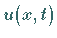 
für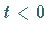 
zu bestimmen, wenn die Werte von 
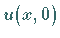gegeben
sind, kann so nicht gelöst werden, weil das CAUCHYsche Problem dann nicht mehr
korrekt gestellt ist.
Da die Temperatur zur Wärmemenge proportional ist, setzt man oft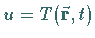 
(Temperaturfeld) und 
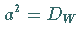(Wärmediffusionskonstante oder Temperaturleitzahl) und
erhält
 |
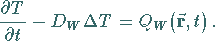(9.106d) |
