Variable obere Integrationsgrenze
1. Partikulärintegral:
Wenn die obere Grenze des Integrals variabel gelassen wird (s. Abbildung mit der Fläche
 ), dann ist die Fläche eine Funktion der oberen Grenze des Integrals, das dann
Partikulärintegral genannt wird.
), dann ist die Fläche eine Funktion der oberen Grenze des Integrals, das dann
Partikulärintegral genannt wird.
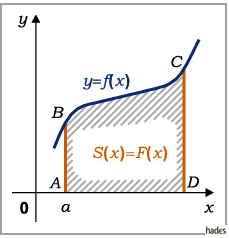
In diesem Falle eines variablen Flächeninhalts spricht man von einer Flächenfunktion
in der Form
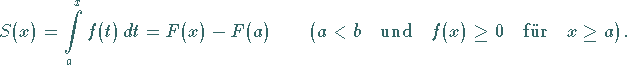 |
(8.41) |
Um Verwechslungen mit der variablen Integrationsgrenze 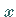 zu vermeiden, wird hier bei
der Darstellung des Integranden die Integrationsvariable mit
zu vermeiden, wird hier bei
der Darstellung des Integranden die Integrationsvariable mit 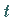 bezeichnet.
bezeichnet.
2. Differentiation des bestimmten Integrals mit variabler oberer Grenze:
Ein bestimmtes Integral mit variabler oberer Integrationsgrenze 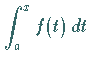 ist eine stetige Funktion
ist eine stetige Funktion 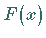 dieser Integrationsgrenze, d.h. die Stammfunktion des
Integranden.
dieser Integrationsgrenze, d.h. die Stammfunktion des
Integranden.
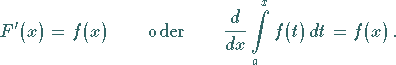 |
(8.42) |
Die geometrische Bedeutung dieses Satzes besteht darin, daß die Ableitung einer
variablen Fläche 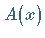 gleich der variablen Endordinate
gleich der variablen Endordinate 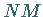 ist (s. Abbildung):
ist (s. Abbildung):
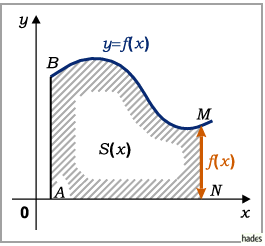
Dabei sind sowohl die Fläche als auch die Ordinate gemäß
Vorzeichenregel mit Vorzeichen zu nehmen.
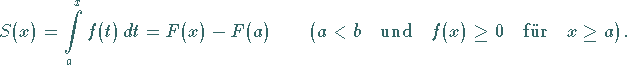
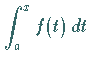 ist eine stetige Funktion
ist eine stetige Funktion ![]() dieser Integrationsgrenze, d.h. die Stammfunktion des
Integranden.
dieser Integrationsgrenze, d.h. die Stammfunktion des
Integranden.
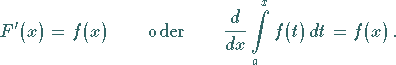
![]() gleich der variablen Endordinate
gleich der variablen Endordinate ![]() ist (s. Abbildung):
ist (s. Abbildung):