|
|
|
|
| (8.18) |
genannt, in dem ![]() und
und ![]() beliebige reelle Zahlen sind und
beliebige reelle Zahlen sind und ![]() beliebige positive oder negative rationale Zahlen.
Der Satz von TSCHEBYSCHEFF besagt, daß das Integral
beliebige positive oder negative rationale Zahlen.
Der Satz von TSCHEBYSCHEFF besagt, daß das Integral
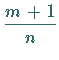 ist eine ganze Zahl Wenn
ist eine ganze Zahl Wenn
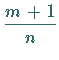 eine ganze Zahl ist, kann das Integral (8.19) durch die
Substitution
eine ganze Zahl ist, kann das Integral (8.19) durch die
Substitution 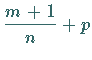 ist eine ganze Zahl Wenn
ist eine ganze Zahl Wenn
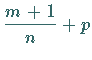 eine ganze Zahl ist, kann das Integral (8.19) durch die
Substitution
eine ganze Zahl ist, kann das Integral (8.19) durch die
Substitution 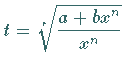 ,
wobei
,
wobei
| Beispiel A | |
|
| |
| Beispiel B | |
|
| |
|
|
|