|
|
|
|
| Integral |
Substitution |
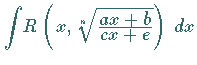 |
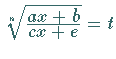 |
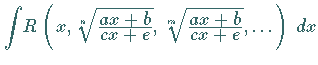 |
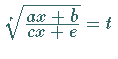 , , |
| wobei |
|
| der Zahlen |
|
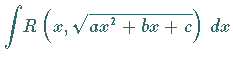 |
Eine der drei EULERschen Substitutionen : |
| 1. Für |
|
| 2. Für |
|
| 3. Falls das Polynom |
|
| schiedene reelle Wurzeln besitzt: | |
|
|
|
| *1) Das Symbol es steht. Die Zahlen |
|
| *2) Ist grand für keinen Wert von von |
|
Das Integral 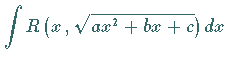 kann auch auf eine der
drei Formen
kann auch auf eine der
drei Formen
gebracht werden, da sich das quadratische Polynom ![]() stets
als Summe oder Differenz zweier Quadrate darstellen läßt.
stets
als Summe oder Differenz zweier Quadrate darstellen läßt.
| Beispiel A | |
|
| |
| Beispiel B | |
|
| |
| Beispiel C | |
|
| |
Die Integrale (8.17a) bis (8.17c) können dann mit Hilfe der in der folgenden Tabelle angegebenen Substitutionen behandelt werden. Sie führen auf Integrale rationaler Ausdrücke, die trigonometrische Funktionen oder Hyperbelfunktionen enthalten.
|
Integral |
Substitution | ||
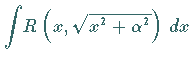 |
oder | ||
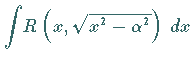 |
oder | ||
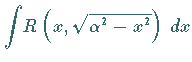 |
oder | ||
|
|
|