4. Fall: Einige Wurzeln des Nenners sind mehrfach komplex

(8.16a)

a) Form der Zerlegung:

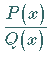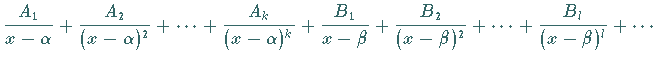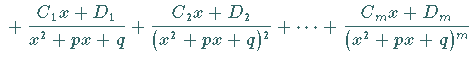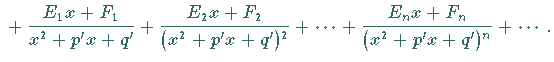			(8.16b)

b) Methode der unbestimmten Koeffizienten: Die Konstanten werden mit Hilfe der Methode der unbestimmten Koeffizienten bestimmt.
c) Integration des Ausdrucks 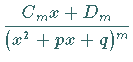mit in folgenden Schritten:
) Umformung des Zählers gemäß

(8.16c)

) Zerlegung des gesuchten Integrals in zwei Summanden, wobei sich der erste direkt integrieren läßt:

(8.16d)

) Der zweite Summand wird ohne den konstanten Faktor mit der folgenden Rekursionsformel berechnet:

			(8.16e)

Beispiel
	. Mit Hilfe der Methode der unbestimmten Koeffizienten ergibt sich das Gleichungssystem , woraus folgt also: . Da gemäß (8.16e) gilt: , ergibt sich schließlich: .