|
|
|
|
mit teilerfremdem Zähler- und Nennerpolynom ist eindeutig in eine Summe von Partialbrüchen der Form
| (1.48) |
Dabei sind ![]() die
die ![]() reellen Wurzeln von
reellen Wurzeln von
![]() .
Außerdem hat
.
Außerdem hat ![]()
![]() Paare konjugiert komplexer Nullstellen, die man
als Nullstellen der quadratischen Faktoren
Paare konjugiert komplexer Nullstellen, die man
als Nullstellen der quadratischen Faktoren ![]() erhält.
Die Zahlen
erhält.
Die Zahlen ![]() sind reell, und es gilt:
sind reell, und es gilt:
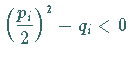 .
.
3. Der Ansatz für die Partialbruchzerlegung lautet:
| Beispiel A | |
|
| |
| Beispiel B | |
|
| |
| Beispiel C | |
|
| |
Hinweis: Hat das Nennerpolynom ![]() nur einfache Wurzeln
nur einfache Wurzeln
![]() ,
dann hat der Ansatz (1.49)
die Form
,
dann hat der Ansatz (1.49)
die Form
| (1.50) |
| Beispiel D | |
|
Es ergibt sich die gleiche Lösung wie in Beispiel A.
| |
|
|
|