Integrale gebrochenrationaler Funktionen
Integrale gebrochenrationaler Funktionen 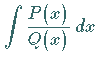 ,
wobei
,
wobei 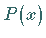 und
und 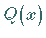 Polynome vom Grade
Polynome vom Grade 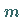 bzw.
bzw. 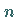 sind, werden algebraisch auf
eine leicht integrierbare Form gebracht.
Dazu dient die folgende Verfahrensweise:
sind, werden algebraisch auf
eine leicht integrierbare Form gebracht.
Dazu dient die folgende Verfahrensweise:
1. Kürzung des Bruches bis 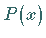 und
und 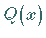 keine gemeinsamen Teiler mehr
enthalten.
keine gemeinsamen Teiler mehr
enthalten.
2. Abspaltung des ganzrationalen Teiles, wenn 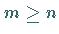 ist, indem
ist, indem 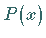 durch
durch 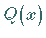 geteilt wird.
Zu integrieren verbleiben dann ein Polynom und ein echter Bruch.
geteilt wird.
Zu integrieren verbleiben dann ein Polynom und ein echter Bruch.
3. Zerlegung des Nenners 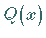 in lineare und quadratische
Faktoren:
in lineare und quadratische
Faktoren:
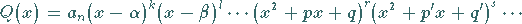 |
(8.12a) |
mit
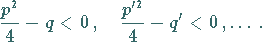 |
(8.12b) |
4. Vorziehen des konstanten Koeffizienten 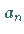 vor das Integralzeichen.
vor das Integralzeichen.
5. Zerlegung in eine Summe von Partialbrüchen: Der so erhaltene echte
Bruch, der nicht mehr gekürzt werden kann und dessen Nenner in seine irreduziblen
Faktoren zerlegt ist, wird in eine Summe von Partialbrüchen zerlegt, die
leicht integriert werden können.
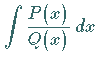 ,
wobei
,
wobei ![]() vor das Integralzeichen.
vor das Integralzeichen.