Wenn ein begrenztes Stück  einer orientierten Fläche auf eine Koordinatenebene
projiziert wird, z.B. auf die
einer orientierten Fläche auf eine Koordinatenebene
projiziert wird, z.B. auf die 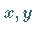 -Ebene, dann kann dieser Projektion
-Ebene, dann kann dieser Projektion 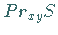 auf
die folgende Weise ein Vorzeichen zugeordnet werden (s. Abbildung).
auf
die folgende Weise ein Vorzeichen zugeordnet werden (s. Abbildung).
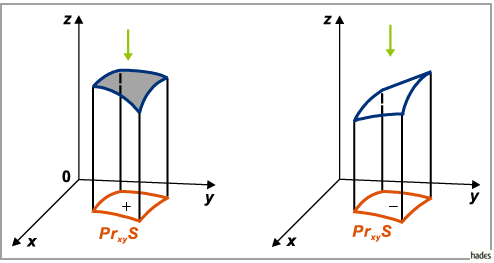
Fällt der Blick von der positiven Seite der 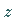 -Achse aus auf die
-Achse aus auf die 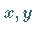 -Ebene und
sieht man dabei die positive Seite des Flächenstückes
-Ebene und
sieht man dabei die positive Seite des Flächenstückes 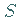 ,
dann gibt man der
Projektion
,
dann gibt man der
Projektion 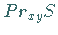 das positive Vorzeichen, im entgegengesetzten Falle das negative
(linke bzw. rechte obere Abbildung).
das positive Vorzeichen, im entgegengesetzten Falle das negative
(linke bzw. rechte obere Abbildung).
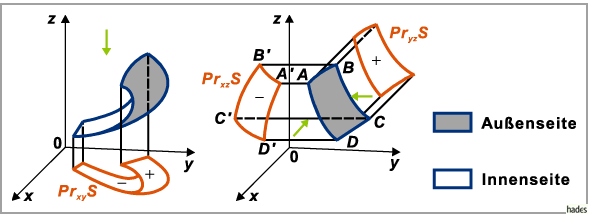
Liegt das Flächenstück so, daß man zum Teil seine Innen- und zum Teil seine
Außenseite sieht, dann ergibt sich 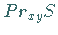 als algebraische Summe der
Projektionen dieser Teile, die einmal von der Innen-, zum anderen von der Außenseite
zu sehen sind (linke untere Abbildung).
Die rechte untere Abbildung zeigt die Projektionen des Flächenstückes
als algebraische Summe der
Projektionen dieser Teile, die einmal von der Innen-, zum anderen von der Außenseite
zu sehen sind (linke untere Abbildung).
Die rechte untere Abbildung zeigt die Projektionen des Flächenstückes 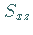 und
und
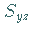 eines Flächenstückes
eines Flächenstückes  ,
von denen die eine negativ, die andere positiv zu
nehmen ist.
,
von denen die eine negativ, die andere positiv zu
nehmen ist.
Die Projektion einer geschlossenen orientierten Fläche ist gleich Null.