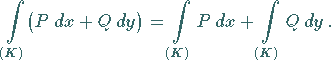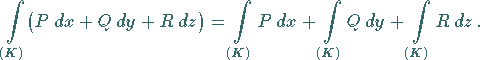Definition des Kurvenintegrals allgemeiner Art
Kurvenintegral allgemeiner Art wird die Summe der Integrale 2. Art über alle
Projektionen einer Kurve genannt.
Wenn entlang des vorgegebenen Kurvenstückes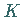 
zwei Funktionen 
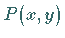und 
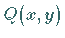von zwei Veränderlichen oder drei Funktionen 
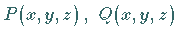und 
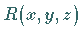von drei Veränderlichen definiert sind und die entsprechenden Kurvenintegrale 2. Art
existieren, dann gilt:
1. Für eine ebene Kurve:
 |
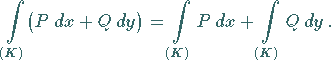(8.118a) |
2. Für eine Raumkurve:
 |
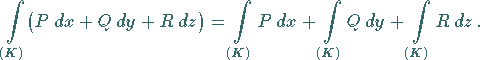(8.118b) |
Die vektorielle Darstellung des Kurvenintegrals allgemeiner Art und eine Anwendung in der
Mechanik wird im Abschnitt ,,Kurvenintegral im Vektorfeld``
behandelt.
