Jede Funktion 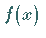 ,
die in einem Intervall
,
die in einem Intervall 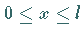 die
DIRICHLETschen Bedingungen erfüllt, kann in diesem Intervall
in konvergente Reihen folgender Formen entwickelt werden:
die
DIRICHLETschen Bedingungen erfüllt, kann in diesem Intervall
in konvergente Reihen folgender Formen entwickelt werden:
Die Periode der Funktion 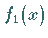 ist
ist 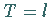 ;
im Intervall
;
im Intervall 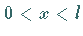 ist
ist 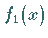 identisch mit der Funktion
identisch mit der Funktion 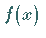 .
.
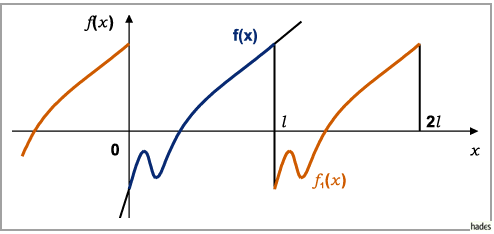
In den Unstetigkeitsstellen wird 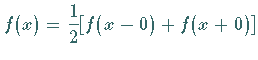 gesetzt.
Die Entwicklungskoeffizienten werden mit Hilfe der
EULERschen Formeln (7.95a,b) für
gesetzt.
Die Entwicklungskoeffizienten werden mit Hilfe der
EULERschen Formeln (7.95a,b) für 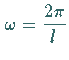 bestimmt.
bestimmt.
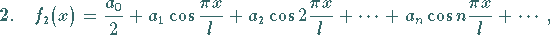 |
(7.105b) |
Die Periode der Funktion 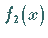 ist
ist  ;
im Intervall
;
im Intervall 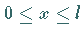 ist
ist 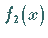 von der Symmetrie S1Art und identisch mit
von der Symmetrie S1Art und identisch mit 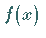 .
.
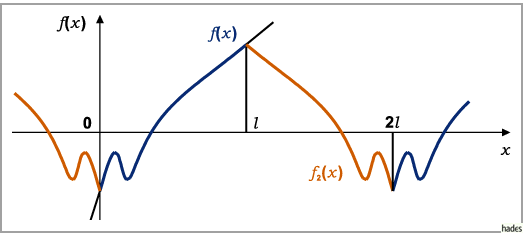
Die Entwicklungskoeffizienten für 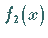 werden nach den Formeln für den Fall der
Symmetrie 1. Art mit
werden nach den Formeln für den Fall der
Symmetrie 1. Art mit  bestimmt.
bestimmt.
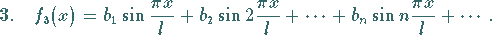 |
(7.105c) |
Die Periode der Funktion 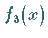 ist
ist 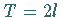 ,
im Intervall
,
im Intervall 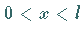 ist
ist
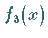 von der Symmetrie 2. Art und identisch mit
von der Symmetrie 2. Art und identisch mit 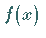 .
.
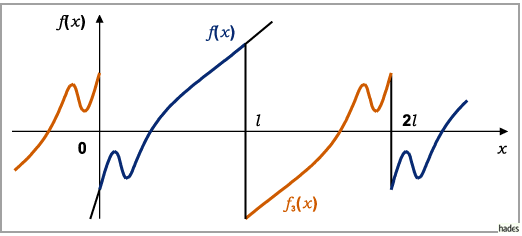
Die Entwicklungskoeffizienten werden mit den Formeln für den Fall der Symmetrie 2. Art
(7.101) für  bestimmt.
bestimmt.
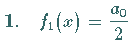
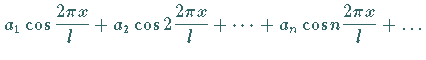
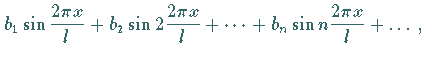
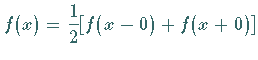 gesetzt.
Die Entwicklungskoeffizienten werden mit Hilfe der
EULERschen Formeln (7.95a,b) für
gesetzt.
Die Entwicklungskoeffizienten werden mit Hilfe der
EULERschen Formeln (7.95a,b) für 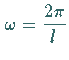 bestimmt.
bestimmt.