Dirichletsche Bedingungen
Wenn die Funktion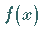 
die DIRICHLETschen Bedingungen erfüllt, d.h. wenn
a) das Definitionsintervall in endlich viele Intervalle zerlegt werden kann,
in denen die Funktion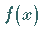
stetig und monoton ist, und
b) an jeder Unstetigkeitsstelle von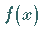
die Werte 
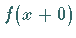und 
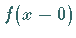definiert sind,
dann konvergiert die FOURIER-Reihe dieser Funktion.
Der Summenwert der Reihe ist dort, wo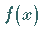
stetig ist, gleich 
,
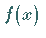in den
Unstetigkeitsstellen gleich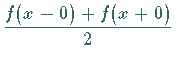 
.
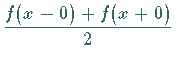