|
|
|
|
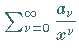 heißt asymptotische
Potenzreihe der Funktion
heißt asymptotische
Potenzreihe der Funktion 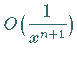 das LANDAU-Symbol
,,groß O`` verwendet.
Für (7.92) schreibt man auch
das LANDAU-Symbol
,,groß O`` verwendet.
Für (7.92) schreibt man auch
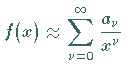 .
.
| Beispiel A | |
|
| |
| Beispiel B | |
|
Wiederholte partielle Integration ergibt für das
Parameterintegral
| |
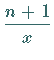 hat.
Trotzdem ist diese divergente Reihe zur Funktionswertberechnung von
hat.
Trotzdem ist diese divergente Reihe zur Funktionswertberechnung von 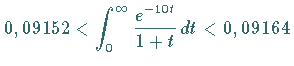 .
.
|
|
|