1. Vertauschung von Gliedern:
a) Die Glieder einer absolut konvergenten Reihe können nach Belieben miteinander
vertauscht werden: Die Reihensumme ändert sich dadurch nicht.
b) Wenn die Glieder einer bedingt konvergenten Reihe so umgestellt werden,
daß in die Umstellung beliebig viele Glieder einbezogen sind, dann kann dadurch die
Reihensumme geändert werden.
Der Satz von RIEMANN besagt, daß auf diese Weise jede beliebige
vorgegebene Zahl zur Reihensumme gemacht werden kann.
2. Addition und Subtraktion:
Absolut konvergente Reihen können gliedweise addiert oder subtrahiert werden.
3. Multiplikation:
Absolut konvergente Reihen können wie gewöhnliche Polynome miteinander multipliziert
werden.
Das Ergebnis ist wieder als Reihe darstellbar, z.B.:
Wenn die Reihensummen 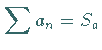 und
und 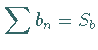 bekannt sind, dann ergibt
sich die Summe der multiplizierten Reihen gemäß
bekannt sind, dann ergibt
sich die Summe der multiplizierten Reihen gemäß
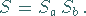 |
(7.35b) |
Wenn zwei Reihen 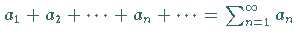 und
und
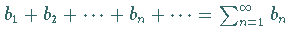 konvergent sind und wenigstens eine
von ihnen absolut konvergiert, dann konvergiert auch die durch Multiplikation aus beiden
erhaltene Reihe.
Sie ist jedoch nicht notwendig ebenfalls absolut konvergent.
konvergent sind und wenigstens eine
von ihnen absolut konvergiert, dann konvergiert auch die durch Multiplikation aus beiden
erhaltene Reihe.
Sie ist jedoch nicht notwendig ebenfalls absolut konvergent.
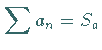 und
und 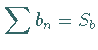 bekannt sind, dann ergibt
sich die Summe der multiplizierten Reihen gemäß
bekannt sind, dann ergibt
sich die Summe der multiplizierten Reihen gemäß
![]() und
und
![]() konvergent sind und wenigstens eine
von ihnen absolut konvergiert, dann konvergiert auch die durch Multiplikation aus beiden
erhaltene Reihe.
Sie ist jedoch nicht notwendig ebenfalls absolut konvergent.
konvergent sind und wenigstens eine
von ihnen absolut konvergiert, dann konvergiert auch die durch Multiplikation aus beiden
erhaltene Reihe.
Sie ist jedoch nicht notwendig ebenfalls absolut konvergent.