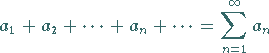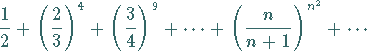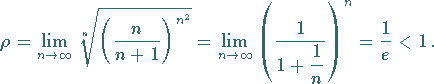Wurzelkriterium von Cauchy
Gilt für eine Reihe
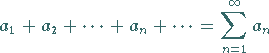 |
(7.28a) |
von einem gewissen 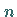 an für alle Zahlen
an für alle Zahlen 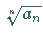
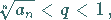 |
(7.28b) |
dann ist die Reihe konvergent.
Sind umgekehrt von einem gewissen 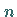 an alle Zahlen
an alle Zahlen 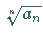 größer als
eine Zahl
größer als
eine Zahl 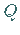 und ist
und ist 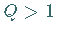 ,
dann divergiert die Reihe.
Daraus ergibt sich: Gilt
,
dann divergiert die Reihe.
Daraus ergibt sich: Gilt
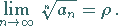 |
(7.28c) |
dann ist die Reihe konvergent für 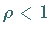 und divergent für
und divergent für 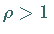 .
Für
.
Für 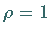 kann mit dem Wurzelkriterium keine Aussage über das Konvergenzverhalten
gemacht werden.
kann mit dem Wurzelkriterium keine Aussage über das Konvergenzverhalten
gemacht werden.
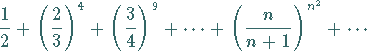 |
(7.29a) |
ist konvergent wegen
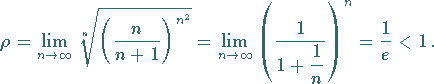 |
(7.29b) |