Relative Extremwerte einer differenzierbaren, explizit gegebenen Funktion
1. Ermittlung der Extrempunkte: Da diese die notwendige Bedingung 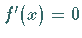 erfüllen, werden nach der Berechnung der Ableitung
erfüllen, werden nach der Berechnung der Ableitung 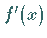 alle reellen Wurzeln
alle reellen Wurzeln
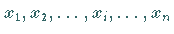 der Gleichung
der Gleichung 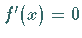 bestimmt und jede von
ihnen, z.B.
bestimmt und jede von
ihnen, z.B. 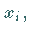 mit einer der folgenden Methoden untersucht.
mit einer der folgenden Methoden untersucht.
2. Methode des Vorzeichenvergleichs:
Für je einen Wert 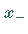 bzw.
bzw. 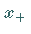 ,
der etwas kleiner bzw. etwas größer als
,
der etwas kleiner bzw. etwas größer als
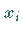 ist, wird das Vorzeichen der Ableitung
ist, wird das Vorzeichen der Ableitung 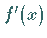 festgestellt, wobei zwischen
festgestellt, wobei zwischen 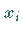 und
und 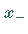 bzw.
bzw. 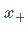 keine weiteren Nullstellen von
keine weiteren Nullstellen von 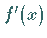 liegen dürfen.
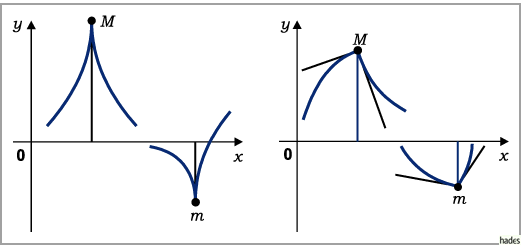
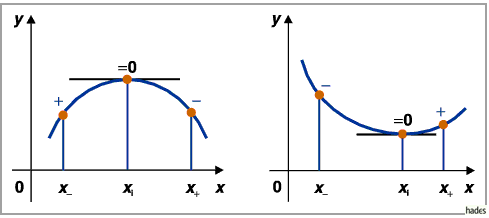
Wenn beim Übergang von
liegen dürfen.
Wenn beim Übergang von 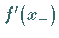 zu
zu 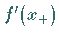 das Vorzeichen von
das Vorzeichen von 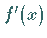 von
,,
von
,,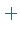 `` nach ,,
`` nach ,,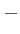 `` wechselt, dann befindet sich bei
`` wechselt, dann befindet sich bei 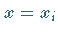 ein
relatives Maximum der Funktion
ein
relatives Maximum der Funktion 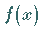 (linke Abbildung); wechselt es umgekehrt von
,,
(linke Abbildung); wechselt es umgekehrt von
,,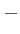 `` nach ,,
`` nach ,,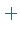 ``, dann liegt ein relatives Minimum vor
(rechte Abbildung).
``, dann liegt ein relatives Minimum vor
(rechte Abbildung).
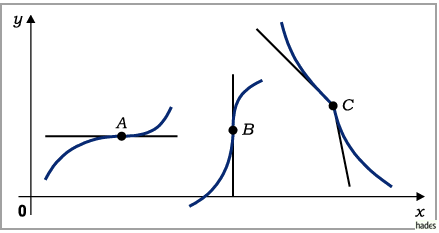
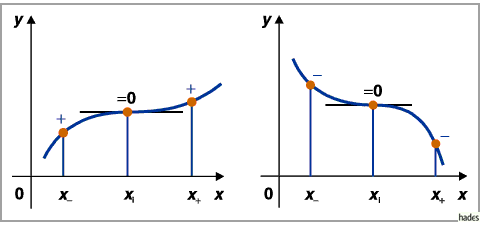
Gibt es keinen Vorzeichenwechsel der Ableitung (folgende linke und rechte Abbildung),
dann besitzt die Kurve bei 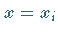 kein Extremum, sondern einen Wendepunkt mit
einer zur
kein Extremum, sondern einen Wendepunkt mit
einer zur  -Achse parallelen Tangente.
-Achse parallelen Tangente.
3. Methode der höheren Ableitungen:
Besitzt die Funktion an der Stelle 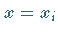 höhere Ableitungen, dann wird jede Wurzel
höhere Ableitungen, dann wird jede Wurzel
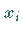 in die zweite Ableitung
in die zweite Ableitung 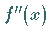 eingesetzt.
Ist
eingesetzt.
Ist 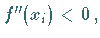 dann gibt es an der Stelle
dann gibt es an der Stelle 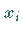 ein relatives Maximum, ist
ein relatives Maximum, ist
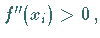 ein relatives Minimum, ist
ein relatives Minimum, ist 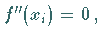 dann wird
dann wird 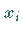 in
die dritte Ableitung
in
die dritte Ableitung 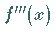 eingesetzt.
Ergibt sich dabei
eingesetzt.
Ergibt sich dabei 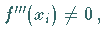 dann gibt es bei
dann gibt es bei 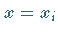 kein Extremum,
sondern einen Wendepunkt .
Erhält man
kein Extremum,
sondern einen Wendepunkt .
Erhält man 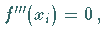 dann ist in die vierte Ableitung einzusetzen usw.
dann ist in die vierte Ableitung einzusetzen usw.
4. Bedingungen für Extremwerte und Wendepunkte:
Ist die Ordnung der Ableitung, die an der Stelle 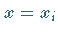 erstmalig nicht verschwindet,
gerade, dann besitzt
erstmalig nicht verschwindet,
gerade, dann besitzt 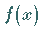 dort ein relatives Extremum:
für einen negativen Wert ein relatives Maximum, für einen positiven ein relatives
Minimum.
Ist die Ordnung dieser Ableitung ungerade, dann besitzt die Funktion an dieser Stelle
keinen Extremwert, sondern einen Wendepunkt .
dort ein relatives Extremum:
für einen negativen Wert ein relatives Maximum, für einen positiven ein relatives
Minimum.
Ist die Ordnung dieser Ableitung ungerade, dann besitzt die Funktion an dieser Stelle
keinen Extremwert, sondern einen Wendepunkt .
Die Methode des Vorzeichenvergleichs kann auch bei nichtexistierender Ableitung wie in
den drei folgenden Abbildungen eingesetzt werden.