Ein relatives Maximum oder Minimum kann bei einer stetigen Funktion nur in den Punkten
auftreten, in denen die Ableitung entweder verschwindet oder nicht definiert ist.
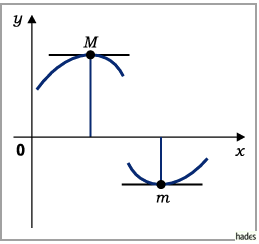
Das bedeutet: In den Kurvenpunkten, die relativen Extremwerten entsprechen, verläuft
die Tangente entweder parallel zur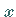 
-Achse (linke Abbildung) oder parallel zur
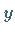-Achse (mittlere Abbildung) oder sie existiert gar nicht (rechte Abbildung).
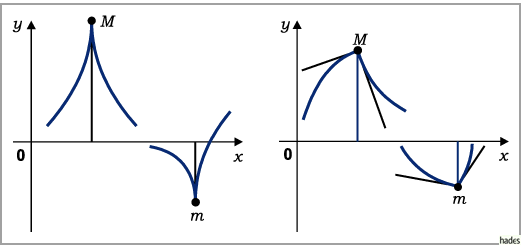
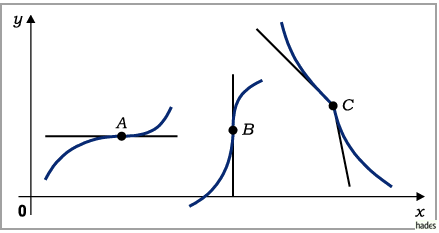
Allerdings handelt es sich hierbei nicht um hinreichende Bedingungen, was an Hand der
Punkte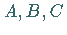 
in der folgenden Abbildung erkennbar ist, für die diese Bedingungen
erfüllt sind, in denen es aber keine Extrema gibt.
Wenn eine stetige Funktion relative Extremwerte besitzt, dann wechseln Maxima und Minima
einander ab, so daß zwischen zwei benachbarten Maxima stets ein Minimum liegt und
umgekehrt.
