Wenn eine Funktion 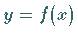 in einem abgeschlossenen Intervall
in einem abgeschlossenen Intervall 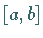 stetig ist,
wenigstens in dem offenen Intervall
stetig ist,
wenigstens in dem offenen Intervall 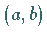 eine Ableitung besitzt und in den Endwerten
des Intervalls den Wert Null annimmt, d.h., wenn
eine Ableitung besitzt und in den Endwerten
des Intervalls den Wert Null annimmt, d.h., wenn
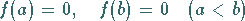 |
(6.28a) |
ist, dann existiert mindestens ein Wert 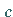 zwischen
zwischen 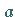 und
und 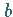 derart, daß gilt
derart, daß gilt
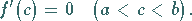 |
(6.28b) |
Die geometrische Bedeutung des Satzes von ROLLE besteht darin, daß eine
Funktion 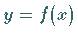 die die
die die 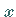 -Achse in zwei Punkten
-Achse in zwei Punkten 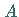 und
und 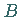 schneidet, in diesem
Intervall stetig ist, und in jedem inneren Punkt eine nichtvertikale Tangente besitzt,
zwischen
schneidet, in diesem
Intervall stetig ist, und in jedem inneren Punkt eine nichtvertikale Tangente besitzt,
zwischen 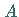 und
und 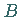 wenigstens einen Punkt
wenigstens einen Punkt 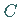 hat, in dem die Kurventangente
parallel zur
hat, in dem die Kurventangente
parallel zur 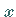 -Achse verläuft (linke Abbildung).
-Achse verläuft (linke Abbildung).
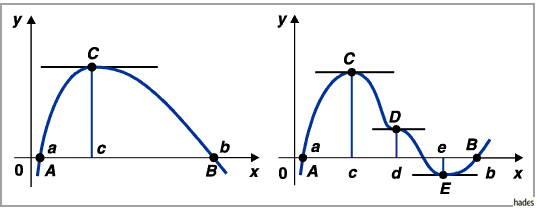
Es kann auch mehrere derartige Punkte in dem Intervall geben, z.B. die Punkte 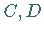 und
und
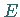 in der rechten Abbildung.
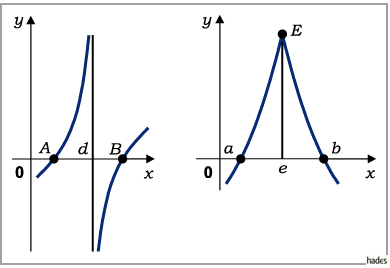
Daß die Forderung nach Stetigkeit und Existenz einer Ableitung in dem Intervall
wesentlich ist, kann an Hand der folgenden linken Abbildung erkannt werden, wo die
Funktion bei
in der rechten Abbildung.
Daß die Forderung nach Stetigkeit und Existenz einer Ableitung in dem Intervall
wesentlich ist, kann an Hand der folgenden linken Abbildung erkannt werden, wo die
Funktion bei  eine Unstetigkeitsstelle besitzt, und an Hand der rechten Abbildung,
wo die Funktion im Punkt
eine Unstetigkeitsstelle besitzt, und an Hand der rechten Abbildung,
wo die Funktion im Punkt 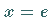 keine Ableitung besitzt.
In beiden Fällen gibt es keinen Punkt
keine Ableitung besitzt.
In beiden Fällen gibt es keinen Punkt 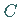 ,
in dem
,
in dem 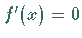 gilt.
gilt.
![]() zwischen
zwischen ![]() und
und ![]() derart, daß gilt
derart, daß gilt
![]() die die
die die ![]() -Achse in zwei Punkten
-Achse in zwei Punkten ![]() und
und ![]() schneidet, in diesem
Intervall stetig ist, und in jedem inneren Punkt eine nichtvertikale Tangente besitzt,
zwischen
schneidet, in diesem
Intervall stetig ist, und in jedem inneren Punkt eine nichtvertikale Tangente besitzt,
zwischen ![]() und
und ![]() wenigstens einen Punkt
wenigstens einen Punkt ![]() hat, in dem die Kurventangente
parallel zur
hat, in dem die Kurventangente
parallel zur ![]() -Achse verläuft (linke Abbildung).
-Achse verläuft (linke Abbildung).