Satz von Fermat

Satz von Fermat

Wenn eine Funktion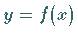

in einem zusammenhängenden Intervall definiert ist und in irgendeinem inneren Punkt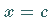

dieses Intervalls ihren größten oder kleinsten Wert besitzt (s. Abbildung), d.h., wenn für alle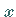

dieses Intervalls gilt

(6.27a)

oder

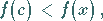(6.27b)

und wenn darüber hinaus ihre Ableitung im Punkt 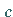existiert, dann kann diese dort nur gleich Null sein:

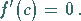(6.27c)

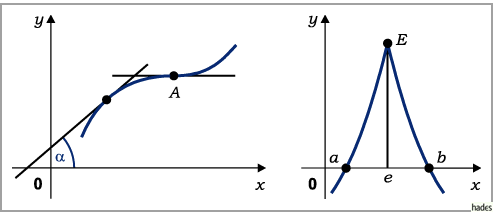
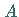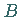Die geometrische Bedeutung des Satzes von FERMAT besteht darin, daß eine Funktion, die den Satz erfüllt, in den Punkten und der Funktionskurve parallel zur 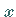-Achse verlaufende Tangenten besitzt (s. Abbildung).

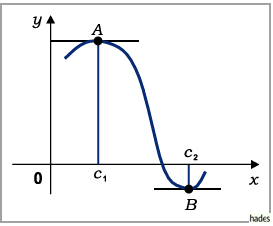
Der Satz von FERMAT stellt aber lediglich eine notwendige Bedingung für die Existenz eines Maximal- oder Minimalwertes einer Funktion in einem Intervall dar. Aus der folgenden linken Abbildung erkennt man, daß die Bedingung nicht hinreichend ist: Im Punkt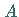

ist zwar

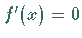erfüllt, aber es gibt weder einen Maximal- noch einen Minimalwert an der Stelle.
Auch die Bedingung der Differenzierbarkeit im Satz von FERMAT ist wesentlich. So hat die Funktion im Punkt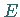

der rechten Abbildung zwar einen Maximalwert, die Ableitung existiert dort aber nicht.