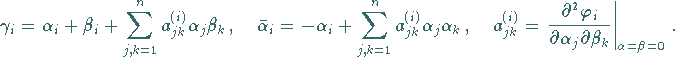Eine kontinuierliche Gruppe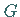 
wird LIE-Gruppe genannt, wenn gilt:
1. Die Gruppenmultiplikation ist kontinuierlich, d.h., zu jeder
Umgebung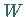 
von 
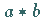gibt es eine Umgebung 
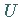von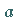 
und eine Umgebung
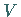von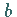 
,
so daß für alle 
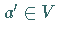auch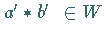 
gilt.
Die Parameter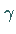 
des Produktelements 
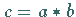sind dann reelle
kontinuierliche Funktionen der Parameter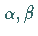 
von
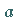bzw.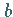 
:
 |
(5.132) |
Die Eigenschaften der Funktionen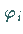 
(s. 
-stellige Operationen), die die Multiplikation in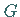
bestimmen, folgen aus den Gruppenaxiomen:
2. Die Funktionen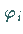
sind beliebig oft stetig differenzierbare
Funktionen aller Parameter
.
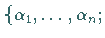
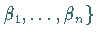Die Funktionen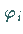
können dann um 
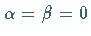(neutrales Element)
in eine TAYLOR-Reihe entwickelt werden.
Bei Beschränkung auf die infinitesimale Umgebung des neutralen Elements und unter
Beachtung der Eigenschaften der Funktionen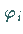
(s. (5.133))
ergibt sich für die Parameter 
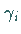des Produktelements
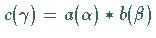und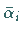 
des inversen Elements
:
 |
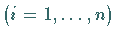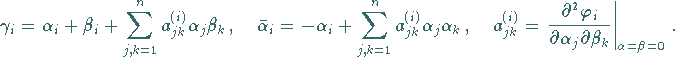(5.134) |
