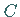|
|
|
|
ein Operator ist, der mit allen Transformationen einer irreduziblen
Darstellung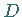 
einer Gruppe kommutiert, d.h., es gilt
,
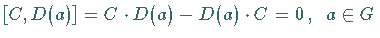und der Darstellungsraum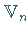 
ein invarianter Unterraum von
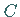ist, dann ist
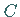ein Vielfaches des Einheitsoperators, d.h. eine Matrix 
,
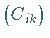die mit allen Matrizen einer irreduziblen Darstellung kommutiert, ist ein Vielfaches
einer Einheitsmatrix 
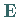also
.
|
|
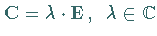