Sind 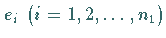 und
und
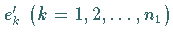 die Basisvektoren der Darstellungsräume
die Basisvektoren der Darstellungsräume
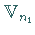 und
und 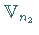 ,
dann bilden die Tensorprodukte
,
dann bilden die Tensorprodukte
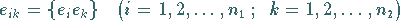 |
(5.122) |
eine Basis im Produktraum 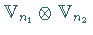 ,
der die Dimension
,
der die Dimension
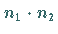 hat.
Aus den Darstellungen
hat.
Aus den Darstellungen 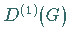 und
und 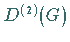 in
in 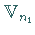 bzw.
bzw. 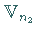 kann man eine
kann man eine 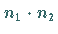 -dimensionale Darstellung
-dimensionale Darstellung 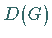 im Produktraum
gewinnen, indem das direkte Produkt oder (innere) KRONECKER-Produkt der
Darstellungsmatrizen bildet:
im Produktraum
gewinnen, indem das direkte Produkt oder (innere) KRONECKER-Produkt der
Darstellungsmatrizen bildet:
Der Charakter des KRONECKER-Produktes zweier Darstellungen ist gleich dem
Produkt der Charaktere der Faktoren
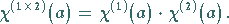 |
(5.124) |