|
Ist 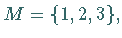 so bezeichnet man die symmetrische Gruppe
so bezeichnet man die symmetrische Gruppe 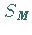 auch mit
auch mit 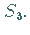 Die
Die 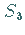 besteht also aus allen bijektiven Abbildungen
(Permutationen) auf der Menge
besteht also aus allen bijektiven Abbildungen
(Permutationen) auf der Menge 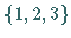 und hat demzufolge
und hat demzufolge
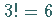 Elemente.
Permutationen werden meist zweizeilig notiert, indem man in die erste Zeile die Elemente
von
Elemente.
Permutationen werden meist zweizeilig notiert, indem man in die erste Zeile die Elemente
von 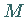 und darunter die jeweiligen Bildelemente schreibt.
So erhält man die 6 Elemente der
und darunter die jeweiligen Bildelemente schreibt.
So erhält man die 6 Elemente der 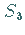 folgendermaßen:
folgendermaßen:
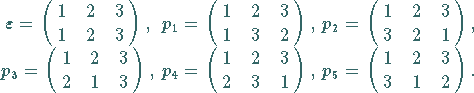 |
(5.96) |
Mit der Hintereinanderausführung (binärer Operationen 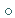 )
von Abbildungen
erhält man für )
von Abbildungen
erhält man für 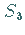 folgende Gruppentafel:
folgende Gruppentafel:
Gruppentafel für 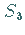
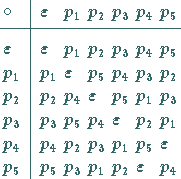 |
(5.97) |
- Aus der Gruppentafel erkennt man, daß die identische Permutation
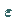 das neutrale Element der Gruppe ist.
das neutrale Element der Gruppe ist.
- In der Gruppentafel kommt jedes Element in jeder Zeile und jeder Spalte genau
einmal vor.
- Das Inverse zu einem Gruppenelement ist aus der Tafel leicht ablesbar; so ist das
Inverse zu
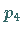 in der
in der 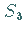 die Permutation
die Permutation 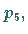 da an der Schnittstelle der
da an der Schnittstelle der
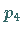 -Zeile mit der -Zeile mit der 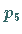 -Spalte das neutrale Element -Spalte das neutrale Element 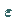 steht.
steht.
- Ist die Gruppenoperation kommutativ ( ABELsche Gruppe), so ist die Tafel
symmetrisch bezüglich der ,,Hauptdiagonalen``; die
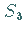 ist nicht kommutativ,
da z.B.
ist nicht kommutativ,
da z.B. 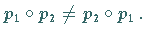
- Das Assoziativgesetz ist aus der Gruppentafel nicht ablesbar.
|