|
|
|
|
| (5.343) |
(E3) Die Gleichheit zweier unscharfer Mengen ![]() und
und ![]() über der
Grundmenge
über der
Grundmenge ![]() ist gegeben, wenn die Werte ihrer Zugehörigkeitsfunktionen gleich
sind:
ist gegeben, wenn die Werte ihrer Zugehörigkeitsfunktionen gleich
sind:
| (5.344) |
(E4) Diskrete Darstellung oder Wertepaardarstellung: Im Falle endlicher
Grundbereiche ![]() d.h.
d.h. ![]() ist es zweckmäßig, die
Zugehörigkeitsfunktionen unscharfer Mengen durch Wertetabellen zu beschreiben:
ist es zweckmäßig, die
Zugehörigkeitsfunktionen unscharfer Mengen durch Wertetabellen zu beschreiben:
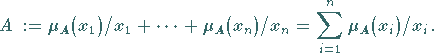 |
(5.345) |
In dieser Definition sind Bruchstriche und Summenzeichen rein symbolisch zu verstehen.
(E5) Ultra-Fuzzy-Sets: Fuzzy-Mengen, deren Zugehörigkeitsgrade
selbst wieder eine Fuzzy-Menge repräsentieren, nennt man nach ZADEH
Ultra-Fuzzy-Sets .
|
|
|