Klassischer Mengenbegriff und unscharfe Mengen
1. Klassische Menge:
Der klassische Mengenbegriff ist zweiwertig, und die klassische BOOLEsche
Mengenalgebra ist isomorph zur zweiwertigen Aussagenlogik.
Zu jeder Menge  über einer Grundmenge
über einer Grundmenge 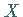 existiert eine Funktion
existiert eine Funktion
 |
(5.341a) |
die für jedes Element 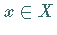 angibt, ob
angibt, ob 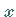 Element der Menge
Element der Menge  ist oder nicht:
ist oder nicht:
 |
(5.341b) |
2. Unscharfe Menge:
Das Konzept der unscharfen Mengen basiert aus logischer Sicht auf der Idee, den
Zugehörigkeitsgrad eines Elements als den graduellen Wahrheitswert einer Aussage im
Intervall 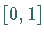 zu betrachten.
Zur mathematischen Modellierung einer Fuzzy-Menge
zu betrachten.
Zur mathematischen Modellierung einer Fuzzy-Menge  benötigt man eine Funktion, die
anstatt in die Menge
benötigt man eine Funktion, die
anstatt in die Menge 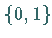 in das Intervall
in das Intervall 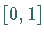 abbildet, d.h.:
abbildet, d.h.:
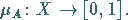 |
(5.342) |
Mit anderen Worten:
Jedem Element 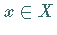 kann eine Zahl
kann eine Zahl 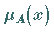 im Intervall
im Intervall 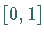 zugeordnet werden,
die den Grad der Zugehörigkeit von
zugeordnet werden,
die den Grad der Zugehörigkeit von 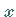 zu
zu  repräsentiert.
Die Abbildung
repräsentiert.
Die Abbildung 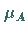 heißt Zugehörigkeitsfunktion .
Der Funktionswert
heißt Zugehörigkeitsfunktion .
Der Funktionswert 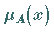 an der Stelle
an der Stelle 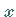 heißt Zugehörigkeitsgrad .
Die unscharfen Mengen
heißt Zugehörigkeitsgrad .
Die unscharfen Mengen 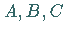 etc. über
etc. über 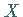 werden auch unscharfe Teilmengen von
werden auch unscharfe Teilmengen von 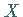 genannt.
Die Gesamtheit aller unscharfen Mengen über
genannt.
Die Gesamtheit aller unscharfen Mengen über 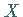 sei mit
sei mit 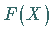 bezeichnet.
bezeichnet.
![]() angibt, ob
angibt, ob ![]() Element der Menge
Element der Menge ![]() ist oder nicht:
ist oder nicht:
![]() zu betrachten.
Zur mathematischen Modellierung einer Fuzzy-Menge
zu betrachten.
Zur mathematischen Modellierung einer Fuzzy-Menge ![]() benötigt man eine Funktion, die
anstatt in die Menge
benötigt man eine Funktion, die
anstatt in die Menge ![]() in das Intervall
in das Intervall ![]() abbildet, d.h.:
abbildet, d.h.:
![]() kann eine Zahl
kann eine Zahl ![]() im Intervall
im Intervall ![]() zugeordnet werden,
die den Grad der Zugehörigkeit von
zugeordnet werden,
die den Grad der Zugehörigkeit von ![]() zu
zu ![]() repräsentiert.
Die Abbildung
repräsentiert.
Die Abbildung ![]() heißt Zugehörigkeitsfunktion .
Der Funktionswert
heißt Zugehörigkeitsfunktion .
Der Funktionswert ![]() an der Stelle
an der Stelle ![]() heißt Zugehörigkeitsgrad .
Die unscharfen Mengen
heißt Zugehörigkeitsgrad .
Die unscharfen Mengen ![]() etc. über
etc. über ![]() werden auch unscharfe Teilmengen von
werden auch unscharfe Teilmengen von ![]() genannt.
Die Gesamtheit aller unscharfen Mengen über
genannt.
Die Gesamtheit aller unscharfen Mengen über ![]() sei mit
sei mit ![]() bezeichnet.
bezeichnet.