|
Im Falle 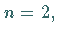 ,
d.h. bei zwei BOOLEschen Variablen ,
d.h. bei zwei BOOLEschen Variablen 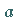 und
und 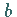 ,
gibt
es 16 verschiedene BOOLEschen Funktionen, von denen die wichtigsten eigene
Namen haben und durch eigene Symbole dargestellt werden.
Sie sind in der folgenden Tabelle aufgeführt. ,
gibt
es 16 verschiedene BOOLEschen Funktionen, von denen die wichtigsten eigene
Namen haben und durch eigene Symbole dargestellt werden.
Sie sind in der folgenden Tabelle aufgeführt.
Tabelle Einige B OOLEsche Funktionen mit zwei Variablen 
und 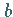
| ![]() ,
d.h. bei nur einer BOOLEschen Variablen
,
d.h. bei nur einer BOOLEschen Variablen ![]() ,
gibt
es die vier BOOLEschen Funktionen:
,
gibt
es die vier BOOLEschen Funktionen: