BOOLEsche Ausdrücke werden induktiv definiert:
Sei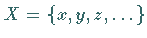 
eine (abzählbare) Menge BOOLEscher Variabler
(die nur Werte aus 
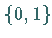annehmen können):
 |
(5.324) |
 |
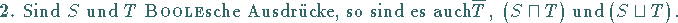(5.325) |
Enthält ein BOOLEscher Ausdruck die Variablen 
so
repräsentiert er eine 
-stellige BOOLEsche Funktion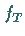 
:
Es sei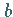 
eine ,,Belegung`` der BOOLEschen Variablen
d.h.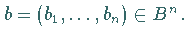 
Unter Beachtung der induktiven Definition werden den Ausdrücken 
wie folgt
BOOLEsche Funktionen zugeordnet:
 |
(5.326a) |
 |
(5.326b) |
 |
(5.326c) |
 |
(5.326d) |
Umgekehrt läßt sich jede BOOLEsche Funktion 
durch einen BOOLEschen
Ausdruck
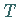darstellen (s. Normalformen).
