|
|
|
|
| (5.318) |
Jede endliche BOOLEsche Algebra ist isomorph zur BOOLEschen Algebra der
Potenzmenge einer endlichen Menge.
Insbesondere hat jede endliche BOOLEsche Algebra ![]() Elemente, und je zwei
endliche BOOLEsche Algebren mit gleich vielen Elementen sind isomorph.
Elemente, und je zwei
endliche BOOLEsche Algebren mit gleich vielen Elementen sind isomorph.
Im folgenden wird mit ![]() die zweielementige BOOLEsche Algebra
die zweielementige BOOLEsche Algebra ![]() mit den folgenden Operationen bezeichnet:
mit den folgenden Operationen bezeichnet:
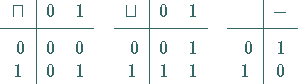
|
|
|