Dualitätsprinzip
1. Dualisieren:
In den im vorhergehenden Abschnitt betrachteten ,,Axiomen`` einer BOOLEschen
Algebra erkennt man folgende Dualität:
Ersetzt man in einem Axiom  durch
durch 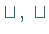 durch
durch  ,
0 durch
1 und 1 durch 0, dann erhält man das jeweils andere Axiom.
Man sagt, diese beiden Axiome sind zueinander dual und nennt den
Ersetzungsprozeß Dualisieren .
Durch Dualisieren erhält man aus einer Aussage über BOOLEsche Algebren die dazu
duale Aussage .
,
0 durch
1 und 1 durch 0, dann erhält man das jeweils andere Axiom.
Man sagt, diese beiden Axiome sind zueinander dual und nennt den
Ersetzungsprozeß Dualisieren .
Durch Dualisieren erhält man aus einer Aussage über BOOLEsche Algebren die dazu
duale Aussage .
2. Dualitätsprinzip für Boolesche Algebren: Die duale Aussage zu einer
wahren Aussage über BOOLEsche Algebren ist wieder eine wahre Aussage über
BOOLEsche Algebren, d.h., mit jeder bewiesenen Aussage ist gleichzeitig auch die
dazu duale Aussage bewiesen.
Aus den Axiomen folgen z.B. folgende Eigenschaften für BOOLEsche Algebren:
(E1) Die Operationen  und
und 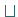 sind idempotent:
sind idempotent:
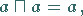 |
(5.313) |
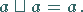 |
(5.314) |
(E2) de Morgansche Regeln:
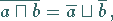 |
(5.315) |
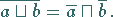 |
(5.316) |
(E3) Eine weitere Eigenschaft:
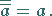 |
(5.317) |
Es genügt auch hier, von jeweils untereinanderstehenden (dualen) Aussagen nur eine zu
beweisen, während die dritte Aussage zu sich selbst dual ist.