Definition der Booleschen Algebra und Grundgesetze
Eine Menge 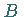 ,
versehen mit zwei binären Operationen
,
versehen mit zwei binären Operationen  (,,Konjunktion``) und
(,,Konjunktion``) und 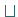 (,,Disjunktion``), einer einstelligen
Operation
(,,Disjunktion``), einer einstelligen
Operation  (,,Negation``) und zwei
ausgezeichneten (neutralen) Elementen
(,,Negation``) und zwei
ausgezeichneten (neutralen) Elementen 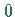 und
und 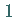 aus
aus 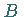 ,
heißt
BOOLEsche Algebra
,
heißt
BOOLEsche Algebra
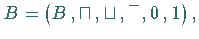 wenn folgende Gesetze gelten:
wenn folgende Gesetze gelten:
(1) Assoziativgesetze:
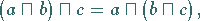 |
(5.299) |
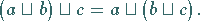 |
(5.300) |
(2) Kommutativgesetze:
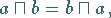 |
(5.301) |
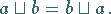 |
(5.302) |
(3) Absorptionsgesetze:
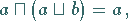 |
(5.303) |
 |
(5.304) |
(4) Distributivgesetze:
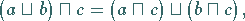 |
(5.305) |
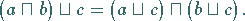 |
(5.306) |
(5) Neutrale Elemente:
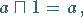 |
(5.307) |
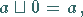 |
(5.308) |
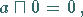 |
(5.309) |
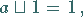 |
(5.310) |
(6) Komplement:
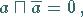 |
(5.311) |
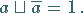 |
(5.312) |
Eine Struktur, in der Assoziativ-, Kommutativ- und Absorptionsgesetze gelten, heißt
Verband .
Gelten darüber hinaus die Distributivgesetze, so spricht man von einem
distributiven Verband .
So ist also eine BOOLEsche Algebra ein spezieller distributiver Verband.
Hinweis Die für BOOLEsche Algebren verwendeten Bezeichnungen der Operationen
sind nicht notwendigerweise identisch mit den in der Aussagenlogik verwendeten Operationen
mit gleicher Bezeichnung.