|
|
|
|
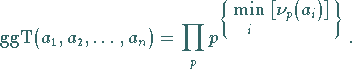 |
(5.250b) |
| Beispiel | |
|
Für die Zahlen | |
1. Euklidischer Algorithmus
Für zwei natürliche Zahlen ![]() kann man den größten gemeinsamen Teiler mit
dem EUKLIDischen Algorithmus ohne Zuhilfenahme der Primfaktorenzerlegung ermitteln.
Dazu ist nach dem folgenden Schema eine Kette von Divisionen mit Rest auszuführen.
Für
kann man den größten gemeinsamen Teiler mit
dem EUKLIDischen Algorithmus ohne Zuhilfenahme der Primfaktorenzerlegung ermitteln.
Dazu ist nach dem folgenden Schema eine Kette von Divisionen mit Rest auszuführen.
Für ![]() sei
sei ![]() Dann gilt:
Dann gilt:
| (5.251b) |
| Beispiel A | |
|
Es gilt | |
| Beispiel B | |
|
| |
| Beispiel | |
|
Der EUKLIDische Algorithmus (s. Formulierung 1 und
Formulierung 2) zur Berechnung des | |
Satz zum Euklidischen Algorithmus
Für natürliche Zahlen ![]() mit
mit ![]() sei
sei ![]() die Anzahl der
Divisionen mit Rest im EUKLIDischen Algorithmus und
die Anzahl der
Divisionen mit Rest im EUKLIDischen Algorithmus und ![]() die Stellenzahl
von
die Stellenzahl
von ![]() im dekadischen System.
Dann gilt:
im dekadischen System.
Dann gilt:
| (5.252) |
| (5.253b) |
| (5.253c) |
| Beispiel | |
|
| |
|
|
|