Begriff des linearen Operators

Begriff des linearen Operators

Es seien

und

zwei Vektorräume. Jede eindeutige Abbildung

von

heißt lineare Abbildung , lineare Transformation oder linearer Operator (s. auch Lineare Operatoren und Funktionale) von

genau dann, wenn gilt:

(5.228)

(5.229)

Beispiel A

Die Abbildung des Raumes der stetigen Funktionen in den der reellen Zahlen ist linear.

Lineare Abbildungen , bei denen wie in diesem Beispiel gilt, werden lineare Funktionale genannt.

Beispiel B

Die Abbildung des Raumes in den Vektorraum der Polynome höchstens -ten Grades ist linear:

Jedem -dimensionalen Vektor wird ein Polynom vom Grade zugeordnet.

Beispiel C

Ist 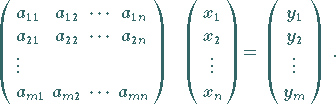und , dann sind alle linearen Operatoren durch reelle Matrizen vom Typ gegeben. Die Gleichung entspricht dem linearen Gleichungssystem (4.104a)

Beispiel A
	Die Abbildung des Raumes der stetigen Funktionen in den der reellen Zahlen ist linear.

Beispiel B
	Die Abbildung des Raumes in den Vektorraum der Polynome höchstens -ten Grades ist linear:

Beispiel C
	Ist und , dann sind alle linearen Operatoren durch reelle Matrizen vom Typ gegeben. Die Gleichung entspricht dem linearen Gleichungssystem (4.104a)