Homomorphismus und Endomorphismus
Seien 
und 
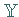zwei Vektorräume über ein und demselben Körper 
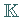und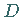 
eine
lineare Teilmenge aus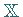 
.
Eine Abbildung 
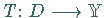heißt linear,
lineare Transformation, linearer Operator oder
Homomorphismus, wenn für beliebige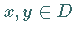 
und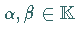 
stets gilt:
 |
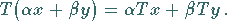(12.20) |
Für einen linearen Operator 
bevorzugt man in Anlehnung an lineare Funktionen die
Bezeichnung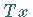 
,
während für allgemeine Operatoren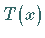 
steht.
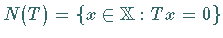ist der Nullraum oder Kern
des Operators
und wird mit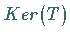 
bezeichnet.
Als Endomorphismus von
bezeichnet man eine lineare Abbildung
des Vektorraumes
in sich.
Ist
eine injektive lineare Abbildung, so ist die aus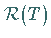 
durch
 |
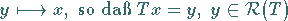(12.21) |
definierte Abbildung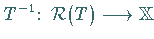 
linear und
heißt Inverse oder Umkehrabbildung von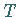 
.
Ist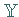
der Vektorraum 
,
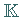so nennt man eine lineare Abbildung
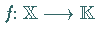ein lineares Funktional oder eine
Linearform.
