Zurückblättern Weiterblättern Übergeordnetes Thema Sachgebiet Hauptinhaltsverzeichnis Stichwortverzeichnis Hilfeseiten        


Symmetrieoperationen in Kristallgitterstrukturen

Unter den Symmetrieoperationen, die das Raumgitter in äquivalente Lagen überführen, sind auch Punktgruppen-Operationen, wie gewisse Drehungen, Drehspiegelungen und Spiegelungen an Ebenen oder Punkten. Allerdings sind nicht alle Punktgruppen auch kristallographische Punktgruppen. Die Forderung, daß die Anwendung der Gruppenelemente auf einen Gittervektor 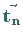wieder einen Gittervektor 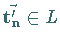(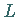: Gesamtheit aller Gitterpunkte) ergeben muß, schränkt die zugelassenen Punktgruppen 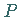mit den Gruppenelemente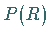n ein:
(5.183)

Dabei bedeutet 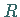einen eigentlichen 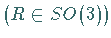oder uneigentlichen Rotationsoperator . Mit einer Gitterstruktur verträglich sind z.B. nur Drehachsen mit der Zähligkeit 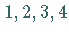oder 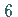. Insgesamt gibt es 32 kristallographische Punktgruppen .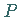
Die Symmetriegruppe eines Raumgitters kann auch Operationen enthalten, die aus einer simultanen Ausführung von Drehungen und primitiven Translationen bestehen. Auf diese Weise erhält man Gleitspiegelungen, d.h. Spiegelungen an einer Ebene und Translationen parallel zur Ebene, und Schraubungen, d.h. Rotation um 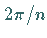und Translationen um 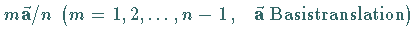. Diese Operationen heißen nichtprimitive Translationen , da sie ,,gebrochenen`` Translationen entsprechen. Bei einer Gleitspiegelung ist 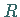eine Spiegelung, bei einer Schraubung ist 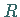eine eigentliche Rotation.
Die Elemente der Raumgruppe 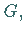, die ein Kristallgitter invariant läßt, setzen sich also aus Elementen 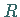der kristallographischen Punktgruppe 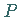, primitiven Translationen 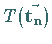und nichtprimitiven Translationen 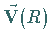zusammen:
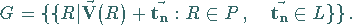(5.184)

Das neutrale Element der Raumgruppe ist , wobei 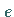das neutrale Element in 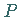bedeutet. Das Element bedeutet eine primitive Translation, 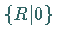steht für eine Drehung oder Spiegelung. Bei der Anwendung des Gruppenelementes 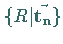auf den Ortsvektor erhält man
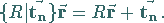(5.185)