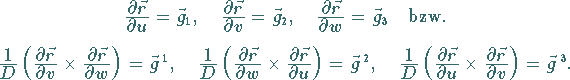|
|
|
|
 |
(4.85) |
Die Darstellung eines Vektors 
lautet dann
 |
(4.86) |
Die Komponenten 
werden als kontravariante Koordinaten, die Komponenten 
als
kovariante Koordinaten des Vektors
bezeichnet.
Zwischen diesen Koordinaten besteht der Zusammenhang
 |
(4.87a) |
mit
 |
(4.88a) |
und daraus folgt
 |
(4.88b) |
Den Übergang von
zu
bzw. von
zu
gemäß (4.87b)
beschreibt man als Heraufziehen bzw. Herunterziehen des Index durch
Überschiebung.
Hinweis: In kartesischen Koordinatensystemen sind kovariante und kontravariante Koordinaten einander gleich.
|
|
