Kovariante Basis

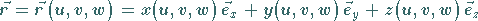(4.82a)

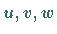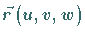werden allgemeine krummlinige Koordinaten eingeführt. Die zu diesem System gehörenden Koordinatenflächen erhält man, indem man in jeweils eine der unabhängigen Variabl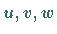en festhält. Durch jeden Punkt des in Frage kommenden Raumteils gehen drei Koordinatenflächen, je zwei schneiden sich in Koordinatenlinien, die durch den betrachteten Punkt hindurchgehen. Die drei Vektoren

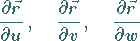(4.82b)

zeigen in die Richtungen der Koordinatenlinien im betrachteten Punkt. Sie bilden die kovariante Basis des krummlinigen Koordinatensystems.