Hauptachsentransformation
Zu einem symmetrischen Tensor
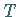 , d.h. für
, d.h. für
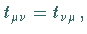 gibt es stets eine orthogonale Transformation
gibt es stets eine orthogonale Transformation 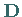 ,
so daß er nach der Transformation Diagonalform hat:
,
so daß er nach der Transformation Diagonalform hat:
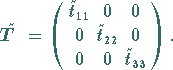 |
(4.77a) |
Die Elemente 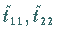 und
und 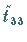 heißen
Eigenwerte des Tensors
heißen
Eigenwerte des Tensors
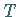 .
Sie sind gleich den Wurzeln
.
Sie sind gleich den Wurzeln 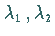 und
und 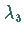 der Gleichung
3. Grades in
der Gleichung
3. Grades in 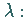
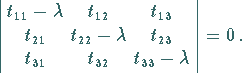 |
(4.77b) |
Die Spaltenvektoren
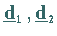 und
und 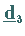 der Transformationsmatrix
der Transformationsmatrix 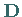 heißen die zu den Eigenwerten gehörenden
Eigenvektoren und genügen den Gleichungen
heißen die zu den Eigenwerten gehörenden
Eigenvektoren und genügen den Gleichungen
 |
(4.77c) |
Ihre Richtungen bezeichnet man als Hauptachsenrichtungen , die Transformation von
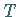 auf die Diagonalform heißt Hauptachsentransformation .
auf die Diagonalform heißt Hauptachsentransformation .
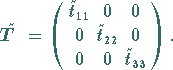
![]() und
und ![]() heißen
Eigenwerte des Tensors
heißen
Eigenwerte des Tensors
![]() .
Sie sind gleich den Wurzeln
.
Sie sind gleich den Wurzeln ![]() und
und ![]() der Gleichung
3. Grades in
der Gleichung
3. Grades in ![]()
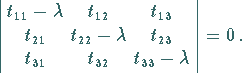
![]() und
und ![]() der Transformationsmatrix
der Transformationsmatrix ![]() heißen die zu den Eigenwerten gehörenden
Eigenvektoren und genügen den Gleichungen
heißen die zu den Eigenwerten gehörenden
Eigenvektoren und genügen den Gleichungen
![]() auf die Diagonalform heißt Hauptachsentransformation .
auf die Diagonalform heißt Hauptachsentransformation .