Rechenregeln
Für Tensoren 2. Stufe gelten dieselben Rechenregeln wie für Matrizen.
Insbesondere läßt sich jeder Tensor
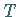als Summe eines
symmetrischen und eines schiefsymmetrischen Tensors darstellen:
 |
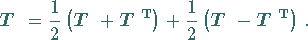(4.76a) |
Ein Tensor
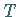
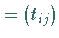heißt symmetrisch , wenn
 |
(4.76b) |
gilt.
Im Falle
 |
(4.76c) |
heißt er schief- oder antisymmetrisch .
Dabei ist zu beachten, daß bei einem antisymmetrischen Tensor die Elemente
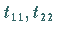und 
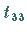Null sind.
Der Begriff der Symmetrie und Antisymmetrie läßt sich auch auf Tensoren höherer
Stufe übertragen, wenn man diese Begriffe auf bestimmte Paare von Indizes bezieht.
