Singulärwerte und Singulärvektoren
Wenn  eine reelle Matrix vom Typ
eine reelle Matrix vom Typ 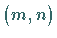 mit dem Rang
mit dem Rang 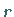 ist, dann heißen
die positiven Wurzeln
ist, dann heißen
die positiven Wurzeln 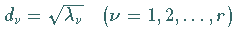 aus den
Eigenwerten
aus den
Eigenwerten 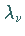 der Matrix
der Matrix  Singulärwerte
der Matrix A.
Die zugehörigen Eigenvektoren
Singulärwerte
der Matrix A.
Die zugehörigen Eigenvektoren 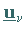 von
von
 heißen Rechtssingulärvektoren von A, die
zugehörigen Eigenvektoren
heißen Rechtssingulärvektoren von A, die
zugehörigen Eigenvektoren 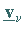 von
von  Linkssingulärvektoren .
Dabei besitzt die Matrix
Linkssingulärvektoren .
Dabei besitzt die Matrix  dieselben
dieselben 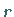 von Null verschiedenen
Eigenwerte
von Null verschiedenen
Eigenwerte 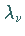 wie die Matrix
wie die Matrix 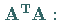
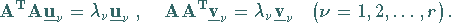 |
(4.152a) |
Außerdem besteht zwischen den Rechts- und Linkssingulärvektoren der Zusammenhang
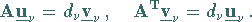 |
(4.152b) |
Es gilt: Eine Matrix  vom Typ
vom Typ 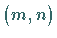 mit dem Rang
mit dem Rang 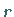 besitzt
besitzt 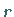 positive
Singulärwerte
positive
Singulärwerte 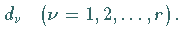 Dazu existieren
Dazu existieren 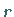 orthonormierte Rechtssingulärvektoren
orthonormierte Rechtssingulärvektoren 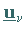 und
und 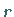 orthonormierte Linkssingulärvektoren
orthonormierte Linkssingulärvektoren 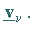 Darüber hinaus existieren zum Singulärwert Null
Darüber hinaus existieren zum Singulärwert Null 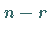 orthonormierte
Rechtssingulärvektoren
orthonormierte
Rechtssingulärvektoren 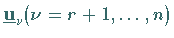 und
und 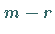 orthonormierte Linkssingulärvektoren
orthonormierte Linkssingulärvektoren
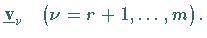 Eine Matrix vom Typ
Eine Matrix vom Typ 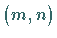 hat demzufolge
hat demzufolge 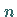 Rechtssingulärvektoren und
Rechtssingulärvektoren und 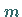 Linkssingulärvektoren, die man zu den orthogonalen Matrizen
Linkssingulärvektoren, die man zu den orthogonalen Matrizen
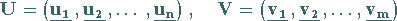 |
(4.153) |
zusammenfassen kann.
![]() vom Typ
vom Typ ![]() mit dem Rang
mit dem Rang ![]() besitzt
besitzt ![]() positive
Singulärwerte
positive
Singulärwerte ![]() Dazu existieren
Dazu existieren ![]() orthonormierte Rechtssingulärvektoren
orthonormierte Rechtssingulärvektoren ![]() und
und ![]() orthonormierte Linkssingulärvektoren
orthonormierte Linkssingulärvektoren ![]() Darüber hinaus existieren zum Singulärwert Null
Darüber hinaus existieren zum Singulärwert Null ![]() orthonormierte
Rechtssingulärvektoren
orthonormierte
Rechtssingulärvektoren ![]() und
und ![]() orthonormierte Linkssingulärvektoren
orthonormierte Linkssingulärvektoren
![]() Eine Matrix vom Typ
Eine Matrix vom Typ ![]() hat demzufolge
hat demzufolge ![]() Rechtssingulärvektoren und
Rechtssingulärvektoren und ![]() Linkssingulärvektoren, die man zu den orthogonalen Matrizen
Linkssingulärvektoren, die man zu den orthogonalen Matrizen