Regularisiertes Problem
Im rangdefizienten Fall , d.h., wenn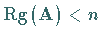 
ist, kann das
Normalgleichungssystem nicht mehr eindeutig gelöst werden, und auch die
Orthogonalisierungsverfahren liefern unbrauchbare Ergebnisse.
Dann geht man an Stelle von (4.119) zu dem sogenannten
regularisierten Problem
 |
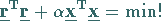(4.121) |
über.
Dabei ist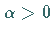 
ein Regularisierungsparameter .
Die Normalgleichungen zu (4.121) lauten:
 |
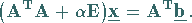(4.122) |
Die Koeffizientenmatrix dieses linearen Gleichungssystems ist für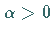
positiv
definit und insbesondere regulär, aber die Wahl eines geeigneten
Regularisierungsparameters 
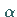ist ein schwieriges Problem (s. Lit. 4.8).
