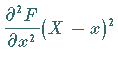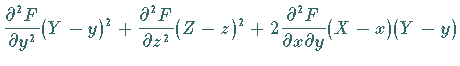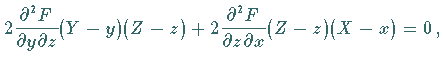Singuläre Flächenpunkte (Kegelpunkte)
Wenn für einen Flächenpunkt mit den Koordinaten 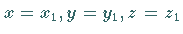 und der Gleichung
und der Gleichung 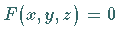 (3.507) gleichzeitig die
Beziehungen
(3.507) gleichzeitig die
Beziehungen
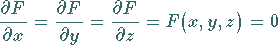 |
(3.519) |
erfüllt sind, d.h. wenn die Ableitungen 1. Ordnung verschwinden, dann ist der Punkt
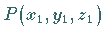 ein singulärer Punkt oder Kegelpunkt .
Alle Tangenten, die durch ihn verlaufen, liegen nicht in einer Ebene, sondern bilden
einen Kegel zweiter Ordnung mit der Gleichung
ein singulärer Punkt oder Kegelpunkt .
Alle Tangenten, die durch ihn verlaufen, liegen nicht in einer Ebene, sondern bilden
einen Kegel zweiter Ordnung mit der Gleichung
in der die Ableitungen im Punkt  zu bilden sind.
Wenn auch alle Ableitungen 2. Ordnung verschwinden, dann handelt es sich um einen
singulären Punkt von komplizierterer Art.
Es liegt also ein Kegel dritter oder höherer Ordnung vor.
zu bilden sind.
Wenn auch alle Ableitungen 2. Ordnung verschwinden, dann handelt es sich um einen
singulären Punkt von komplizierterer Art.
Es liegt also ein Kegel dritter oder höherer Ordnung vor.