Definitionen
1. Tangentialebene: Wenn durch einen Flächenpunkt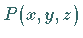 
alle auf
dieser Fläche möglichen Flächenkurven hindurchlaufen, dann liegen in der Regel
alle zugehörigen Kurventangenten im Punkt 
in ein und derselben Ebene, der
Tangentialebene der Fläche des Punktes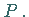 
Ausgenommem davon sind die sogenannten Kegelpunkte.
2. Flächennormale: Eine Gerade, die senkrecht auf der Tangentialebene
steht und durch den Punkt
verläuft, heißt Flächennormale im
Punkt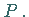
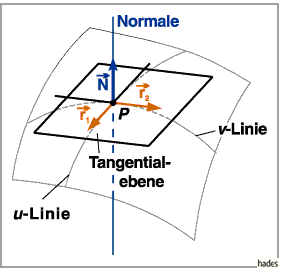
3. Normalenvektor: Die Tangentialebene wird von zwei Vektoren aufgespannt,
den Tangentenvektoren
 |
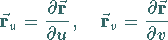(3.514a) |
der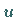 
- und der 
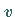-Linie.
Das Vektorprodukt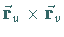 
der beiden Tangentenvektoren
ist ein Vektor, der in die Richtung der Flächennormalen weist.
Sein Einheitsvektor
 |
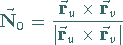(3.514b) |
wird Normalenvektor genannt.
Seine Richtung nach der einen oder anderen Seite der Fläche ist dadurch festgelegt,
ob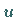
oder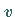
erste oder zweite Koordinate ist.
