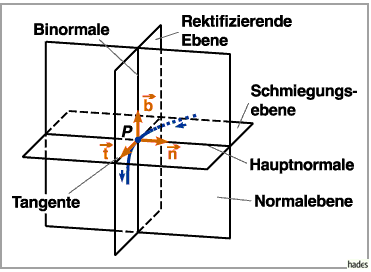
Geraden und Ebenen in einem Punkt der Raumkurve
In jedem Punkt 
einer Raumkurve, mit Ausnahme der singulären Punkte, können drei
Geraden und drei Ebenen definiert werden, die sich im Punkt
schneiden und senkrecht
aufeinander stehen:
1. Tangente ist die Grenzlage der Sekante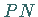 
für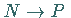 
.
2. Normalebene ist eine Ebene, die senkrecht auf der Tangente steht.
Alle durch
verlaufenden und in dieser Ebene liegenden Geraden werden die
Normalen der Kurve im Punkt
genannt.
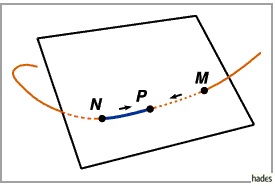
3. Schmiegungsebene wird die Grenzlage einer Ebene genannt, die durch drei
benachbarte Kurvenpunkte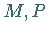 
und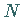 
verläuft, für die 
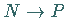und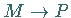 
geht.
In der Schmiegungsebene befindet sich die Kurventangente.
4. Hauptnormale nennt man die Schnittgerade von Normalen- und Schmiegungsebene,
d.h., es ist die Normale, die in der Schmiegungsebene liegt.
5. Binormale wird die Senkrechte auf die Schmiegungsebene genannt.
6. Rektifizierende Ebene heißt die von der Tangente und der Binormalen
aufgespannte Ebene.
Die positiven Richtungen werden auf den drei Geraden (1.), (4.) und (5.)
folgendermaßen festgelegt:
a) Auf der Tangente ist es die positive Richtung der Kurve, die durch
den Tangenteneinheitsvektor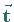 
festliegt.
b) Auf der Hauptnormalen ist es die Richtung der Kurvenkrümmung, festgelegt
durch den Normaleneinheitsvektor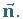 
c) Auf der Binormalen ist sie durch den Einheitsvektor
 |
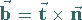(3.491) |
definiert, wobei die drei Vektoren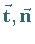 
und 
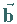ein
rechtshändiges Koordinatensystem bilden, das begleitendes Dreibein der Raumkurve
genannt wird.
