Paraboloide
Da Paraboloide keinen Mittelpunkt besitzen, wird in den folgenden Gleichungen davon
ausgegangen, daß der Scheitel des Paraboloids im Koordinatenursprung liegt, die
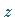 -Achse zur Symmetrieachse wird und die
-Achse zur Symmetrieachse wird und die 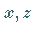 - sowie die
- sowie die 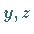 -Ebenen
Symmetrieebenen sind.
-Ebenen
Symmetrieebenen sind.
a) Elliptisches Paraboloid:
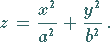 |
(3.435) |
Ebenenschnitte parallel zur 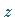 -Achse liefern als Schnittfiguren Parabeln, parallel zur
-Achse liefern als Schnittfiguren Parabeln, parallel zur
 -Ebene Ellipsen.
-Ebene Ellipsen.
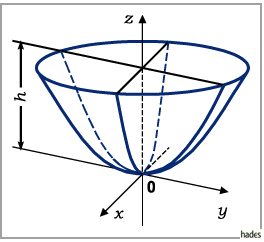
b) Rotationsparaboloid:
Für 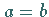 erhält man ein Rotationsparaboloid, das man sich durch Rotation einer
Parabel mit
erhält man ein Rotationsparaboloid, das man sich durch Rotation einer
Parabel mit 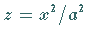 um ihre in der
um ihre in der 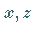 -Ebene liegende Achse entstanden denken
kann.
-Ebene liegende Achse entstanden denken
kann.
Der Rauminhalt eines Paraboloidschale, die von einer Ebene senkrecht zur 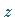 -Achse in
der Höhe
-Achse in
der Höhe 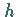 abgeschnitten wird, ist
abgeschnitten wird, ist
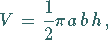 |
(3.436) |
d.h., halb so groß wie der Rauminhalt des elliptischen Zylinders mit der
gleichen Deckfläche und Höhe.
c) Hyperbolisches Paraboloid:
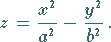 |
(3.437) |
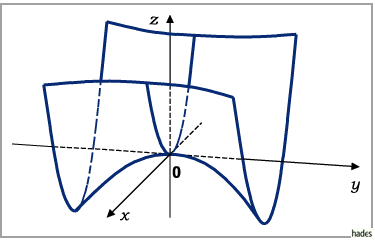
Schnitte parallel zur  -Ebene und zur
-Ebene und zur 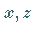 -Ebene liefern kongruente Parabeln als
Schnittfiguren, Schnitte parallel zur
-Ebene liefern kongruente Parabeln als
Schnittfiguren, Schnitte parallel zur 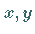 -Ebene Hyperbeln sowie ein Paar einander
schneidender Geraden.
-Ebene Hyperbeln sowie ein Paar einander
schneidender Geraden.