|
|
|
|
| Größen |
Gestalt der Kurve | ||
| Mittelpunktskurven
|
Ellipse
a) für b) für |
||
| Ein Paar imaginäre mit reellem Punkt |
|||
| Hyperbel | |||
| Ein Paar sich schneidender Geraden | |||
| Notwendige Koordinatentransformation | Normalform der Gleichung nach Transformation |
1. Verschiebung des Koordinatenursprungs in
|
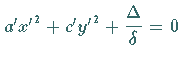 |
2. Drehung der Koordinatenachsen um den
|
|
|
|
|