1. Allgemeine Gleichung der Kurven 2. Ordnung
Mit der allgemeinen Gleichung der Kurven 2. Ordnung
 |
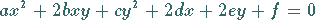(3.374a) |
werden die Ellipse, ihr Spezialfall der Kreis, die Hyperbel, die Parabel oder ein
Geradenpaar (zerfallende Kurve 2. Ordnung) definiert.
Die Rückführung auf die Normalform kann mit Hilfe der in den Tabellen
Transformation der Kurvengleichungen 2. Ordnung auf die Normalform, Mittelpunktsgleichungen
und
Transformation der Kurvengleichungen 2. Ordnung auf die Normalform, parabolische Gleichungen
angegebenen Koordinatentransformationen erreicht werden.
Hinweis: Die Koeffizienten in der obigen Gleichung (3.374a)
sind nicht identisch mit den Parametern der speziellen Kegelschnitte in den Gleichungen
für die Ellipse, Hyperbel und Parabel.
2. Invariante einer Kurve 2. Ordnung
Invariante einer Kurve 2. Ordnung sind die drei Größen
 |
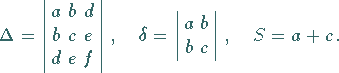(3.374b) |
Bei Drehungen des Koordinatensystems bleiben sie erhalten, d.h., wenn nach einer
Koordinatentransformation die Kurvengleichung die Form
 |
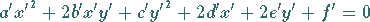(3.374c) |
hat, dann liefert die Berechnung dieser drei Größen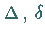 
und 
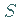aus den neuen Konstanten die ursprünglichen Werte.
3. Gestalt der Kurven 2. Ordnung (Kegelschnitte)
Wenn ein gerader Kreiskegel von einer Ebene geschnitten wird, dann entsteht auf ihr ein
Kegelschnitt.
Geht die schneidende Ebene nicht durch die Spitze, dann ergibt sich eine Hyperbel, Parabel
oder Ellipse in Abhängigkeit davon, ob die Ebene parallel zu zwei, nur zu einer oder zu
keiner Erzeugenden des Kegels verläuft.
Geht die schneidende Ebene durch die Kegelspitze, dann entstehen
zerfallende Kegelschnitte mit 
Als Kegelschnitt eines in einen Zylinder entarteten Kegels , dessen Spitze sich
im Unendlichen befindet, ergeben sich zwei parallele Geraden.
Der Bestimmung der Gestalt der Kegelschnitte dienen die Tabellen
Transformation der Kurvengleichungen 2. Ordnung auf die Normalform, Mittelpunktsgleichungen
und
Transformation der Kurvengleichungen 2. Ordnung auf die Normalform, parabolische Gleichungen.
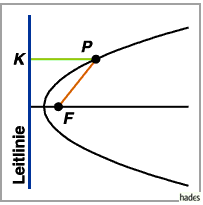
4. Leitlinieneigenschaft der Kurven 2. Ordnung
Der geometrische Ort aller Punkte 
mit einem konstanten Verhältnis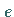 
der
Abstände zu einem festen Punkt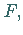 
dem Brennpunkt, und zu einer gegebenen Geraden,
der Leitlinie, ist eine Kurve 2. Ordnung mit der numerischen Exzentrizität
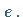
Für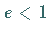 
ergibt sich eine Ellipse, für 
eine Parabel und für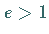 
eine
Hyperbel.
5. Bestimmung der Kurve durch fünf Punkte
Durch fünf vorgegebene Punkte kann eine und nur eine Kurve 2. Ordnung gehen.
Wenn drei dieser Punkte auf einer Geraden liegen, dann ergibt sich ein
zerfallender Kegelschnitt .
6. Polargleichung der Kurven 2. Ordnung
Alle Kurven 2. Ordnung werden mit der einen Polargleichung
 |
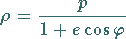(3.375) |
beschrieben, wobei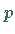 
der Halbparameter und
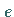die Exzentrizität sind.
Dabei liegt der Pol im Brennpunkt, während die Polarachse vom Brennpunkt nach dem
nächstgelegenen Scheitelpunkt hin gerichtet ist.
Für die Hyperbel definiert diese Gleichung nur einen Ast.
