|
|
|
|
Größen 
und  |
Gestalt der Kurve | |
Parabolische Kurven
 |
 |
Parabel |
 |
Geradenpaar
Parallele Geraden für 
Doppelgerade für 
Imaginäre Gerade für  |
|
| Notwendige Koordinatentransformation | Normalform der Gleichung
nach Transformation |
| 1. Verschiebung des Koordinatenursprungs in
den Scheitel der Parabel, dessen Koordinaten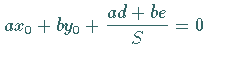 
und 
durch die Gleichungen
und
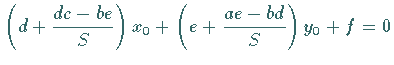
definiert werden. 2. Drehung der Koordinatenachsen um den Winkel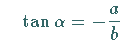 
mit  ;
das Vorzeichen von 
muß dem Vorzeichen
von 
entgegengesetzt sein. |
 |
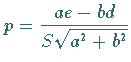| Drehung der Koordinatenachsen um den Winkel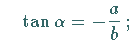
mit 
das Vorzeichen von
muß dem Vorzeichen
von
entgegengesetzt sein. |
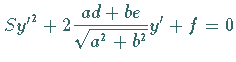ist auf die Form 
transformierbar. |
Im Falle
wird vorausgesetzt, daß keiner der
Koeffizienten 
verschwindet.
Der Kurvengleichung entspricht eine imaginäre Kurve.
Hinweis: Sind zwei Koeffizienten (
und 
oder
und 
so reduzieren
sich die notwendigen Koordinatentransformationen auf eine Verschiebung der
Koordinatenachsen.
Die Gleichung 
erhält die Form
die Gleichung 
erhält die Form
|
|